PCA – Testing for significance

One of the reasons to perform Principal Component Analysis is to perform feature extraction, identify significan variables based on its variance. Following that idea PCA tackles that goal from the beginning. Eve when we could perform the analysis using all the variables we don’t do that. The reason is that not all variables bring significance in terms of its association to other variables. And how do we test the association to other variables? Through the correlation.
PCA identifies how the variables change together, those with no correlation may actually be a component itself, so we test for significance in order to select variables that give significance to the analysis.

Testing for significance

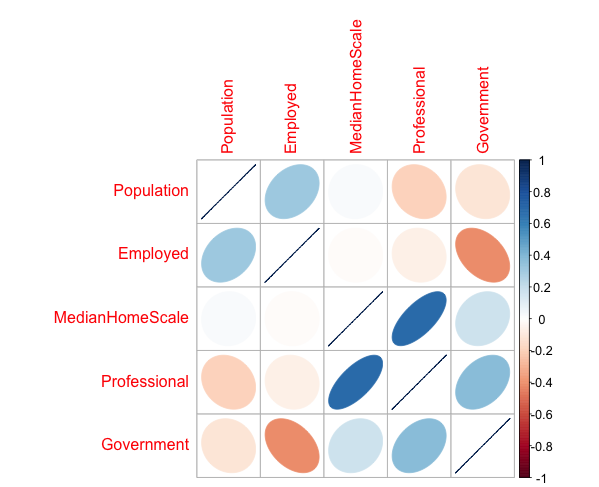
We perform a test of the correlation. Plotting the correlation matrix we may see variables that have strong associations. Consider the times for completing different run distance races from 100m, 400m up to 10ks and even marathons. There most be more correlation between the long distance races,10k 21k a marathon. On the other hand sprint races may have stronger associations and there may be a middle point for the 1/4 mile to 5ks.

Testing for significance in the correlation let us know two things: 1) Give us an idea of how many
components we have(long distance, sprint distance etc.). 2) Identify variables that are uncorrelated to other variables (possible components) or highly correlated to many (noisy variables, would not be considered).

We may use R to perform the correlation test using the function corr.test() for the library Psych. The function allows you to set the level you desire to test upon. One of its outputs is the two tail probability for each correlation. With that we only nee to se how many significant correlations we have (how many probabilities are lower than the desire level).

If all variables have the same number then all variables should be considere. Variables that have only one significant correlation will be drop from the analysis, but keep in mind that this variables may be a component. There may be variables that have many more significant correlations to other variables, those variables are noisy and may fall into all components, so we would drop them too.
So we would select the variables that are in the middle point to proceed with the analysis.

Imagine that this is the result for the run races:
# of Significant Correlations
100m 3
200m 3
400m 2
800m 2
3k 1
5k 8
10k 3
21k 2
42k 2

We would drop 3k, may be a component. Drop 5k, as is correlated to all variables. And take to the next step all other variables.
A little help in the R code
RunTest = corr.test(RunRacesData,alpha = 0.05,adjust = ‘none’)
RT=RunTest$p
Significance= ifelse(RT colSums(CensusSignificance)-1 #Subtract 1 as the correlation of each variable to itself is significant

This are corrplots, correlation matrixes plots. Strong correlations are shown with a thin dark color ellipse.